Recently I was asked to talk at a secondary school about mathematics and mathematical philosophy. The following is roughly based on what I talked about…
I was asked to come and talk to you about mathematics, which is lucky, because I’m a mathematician. But then I wondered what exactly I should tell you.
I thought — well, should I give you a maths class? But I figure that’s probably not the best idea. I might talk about a little bit of actual maths, but don’t worry, there will be no test.
Then I thought — should I try to persuade you to study more maths? A sales pitch for mathematics? Well, I’m sure you’ve all had an excellent education here, in mathematics as in every other subject, so there’s no need for further persuasion. And anyway I’m not much of a salesman. However, I might try to show you a couple of things about maths that I think makes it interesting
Then I thought — should I tell you about all the places maths is useful in everyday life? Well, maths does come up pretty much everywhere, and it’s used by people all the time – sometimes with good effect, sometimes bad, but in any case it’s everywhere. So I might talk a little about that too. And It raises all sorts of big philosophical questions.
And speaking of philosophy — in the philosophy of mathematics there are all sorts of deep, abstract, and interesting questions there. Pretty heavy ones too. What does it mean for a mathematics to be true? What is mathematics anyway? Well, those are pretty deep questions, but since I’m the only professional mathematician in the room, I might say a little about it.
Then I thought — I’m just here to talk to you. And as far as I’m concerned I’m talking to adults.
But then I thought — oh, I should probably introduce myself first! Well it would be rude not to, so OK, I’ll do that first, then I’ll tell you some of the things I think about mathematics, which are hopefully kind of interesting. And then we’ll leave some time for questions, and you can ask me about anything you like.
* * *
So yes, I will start by telling you a little bit about myself. I’m a mathematician, a lecturer at Monash Uni. I’m also, a sometime lawyer, activist, writer, husband, dog owner.
I’ve been into maths since I was very young. At school I enjoyed learning lots of things, including mathematics and science. I’ve always wanted to know how the world works. But actually my favourite subject at school was history. You know, “maths, science, history – unravelling the mystery”. I heard that on TV somewhere. I enjoyed history: learning about how we came to be how we are now – how we got into this mess!
At school I found out I was apparently good at maths, and I got involved in the Maths Olympiad. I actually represented the country at the International Maths Olympiad.
I graduated from school, feeling like I didn’t know anything, and that there was so much more to learn. I went to university. I wanted to learn everything, but they only let me enrol in two degrees. So I studied science and law: the rules that govern the world, and the rules that govern society. And from then on I’ve never really left university, but I still feel like I know nothing. I did a few courses here in Melbourne, then I did a PhD in maths at Stanford University in California. I got involved in some politics as well – I was involved in a website you might have heard of called Wikileaks, although I left it long ago, before it became famous, or rather, infamous. After getting my PhD I then worked in France, at the University of Nantes – Nantes is a city in north-western France which has good mathematicians and good crepes. Then I worked in Boston, at a university called Boston College. So as you can see mathematics is very international. It’s the same with all science really – it’s a very international enterprise.
I now work at Monash Uni, in the maths department there. I am also a fully qualified lawyer, and although I’ve never practised law, I have done volunteer legal work and been involved in some politics here as well. I’m an advisor, for instance, to a wonderful group called the Initiative for Equality, which works to build more equal and participatory societies around the world.
But that’s enough about myself. If you want to know anything more you will have to ask.
* * *
So, let’s get down to talking a bit about mathematics. And I thought a first thing to do might be to actually ask – what is mathematics? Because I suspect the average person, and you, and me, might all have different answers.
As a mathematician, I think it’s actually quite a difficult thing to define.
Perhaps the main thing I want to impress upon you about what mathematics is, is just how big it is, how long it’s been going, and how narrow a slice of it most people see. Maths is a lot more than the subject you learn at school called maths!
Studying maths at school, you can kind of get the impression that you study year 7 maths, and then year 8 maths, and so on, and finally you get to year 12 maths, and you are then done. You finished mathematics.
Well, no. At that point you know a little bit of the mathematics that was known up to the 17th century. You’ve seen essentially zero mathematics from the last 300 years – possibly a little bit, if you’ve got good teachers, as I’m sure you do here.
But what would your education be like, if you graduated from school completing all the English units, but never having studied, let alone read or even seen, any literature from after 1700? Well with mathematics it’s like that.
Perhaps it’s not quite that bad. Mathematics doesn’t change like English does. Literature from 1700 is now outdated, in a certain sense, but mathematics from 1700 is not. It’s just as true, just as valid now as it was then. And mathematics had made a significant amount of progress by 1700, so it’s not terribly bad that you only get up to 1700.
But it’s useful to place it in context. Mathematics has an enormously long and rich history, and its story goes right back to the beginning of civilization. We have evidence of writing numbers dating from about 3500 BC. The Sumerians were doing their times tables from 2500 BC. The ancient Egyptians knew about prime numbers before 1800 BC.
But mathematics exploded in ancient Greece from the 6th century BC onwards and took the world by storm. And since then, mathematics has been actively advancing.
Told you I liked history.
But whenever you are learning mathematics, you are tapping into one of the deepest continuous strains of human thought, and you are tapping into some of the most ingenious, clever, ideas ever conceived, ideas developed by some of the greatest minds in history.
Think of it this way. We are now so advanced that, in a mere 12 or 13 years of schooling, you’re able to go from a pre-literate level of mathematical understanding, up to the 17th century. That’s quite an achievement. It took humanity millennia, but for you it’s just exercises in your textbook – combined with good teachers.
So maths has been around a long time. It’s not going away – sorry if you don’t like it. It was here before we were born, it will still be here after we are gone. It will even survive Donald Trump. And it will be no less true for that.
* * *
So, what is mathematics? In the end I can’t really define it, but I can say some things that are mathematics and some things that are not.
Now, there are many things we know that are definitely included in mathematics. Algebra is maths. Geometry is maths. Anything with numbers in it is maths. Anything with exact logic in it is maths – maths has a type of thinking and a type of logic that is characteristic to the subject, and unlike the sort of thinking you get pretty much anywhere else – we might talk more about that later.
Some other things are definitely not mathematics. History is not maths. Biology, chemistry, physics are not maths, although they may use it. Physics is an interesting one actually – it’s very mathematical, and so much so that sometimes the boundary between physics and mathematics is unclear. I might talk more about that later.
The other sciences are easier to define than maths. You can say at least roughly what these other sciences are about. Physics is about the study of objects in the universe and so on, chemistry is about the properties of atoms and molecules and their reactions and so on.
The other sciences are easier to define because they’re basically limited to things which actually exist in this universe. Maths, on the other hand, has no such limitations. It does have some limitations. It shouldn’t be wrong. Two and two is definitely not five. Other than that, it’s limited only by our imagination.
* * *
Let me try to give you an idea of what I think mathematics is by giving you an example of the type of outlook a mathematician has.
Suppose a mathematician walks into a bar. This is not a joke… much…
In the bar there is a pool table. But as you’re all underage, you don’t know this.
 (Source)
(Source)
For those of you who haven’t played pool, the idea is to hit these billiard balls into the pockets using a cue stick. The exact rules aren’t important here, the point here is simply that the balls roll around on the table, bounce off the sides, hit each other, and so on.
Anyway, a lot of mathematics has been inspired by pool tables. And this is not (just) because mathematicians drink too much.
A mathematician might look at a pool table and see some interesting geometry problems – to get this ball into that pocket, where should you aim? Well perhaps you can do a reflection like this, and aim over there.
 (Source)
(Source)
And she might go further, and wonder, what can you say about the path, the trajectory traced out by a billiard ball? Is it possible for a ball to start off in one position, going in a particular direction, and later come back to that position going in the same direction? Can it do so after hitting every wall? Is it possible to hit the wall 17 times and come back to your initial position and direction? Is it possible for a billiard ball to go in such a way that it eventually passes through every point on the table?
 (Source)
(Source)
What if you change the geometry of the table – make it a triangle, or a square, or a pentagon, or even make it curved? What if it’s a concave heptagon?
 (Source)
(Source)
What if it’s 3-dimensional?
 (Source)
(Source)
So, by pure imagination, you have a dozen questions all ready to think about. They belong to different fields of mathematics, some of which you may never have seen. But somehow they’re all mathematical questions. Some of them are much harder than others. Some might require more advanced ideas, or ideas that haven’t even been invented yet. Others might be impossible.
But the point I’m making is that mathematician is free to ask whatever questions she pleases. She is limited only by her imagination. She invents her own problems, and tries to solve them. She solves the ones she likes. She solves the ones she can.
In the meantime, everyone else in the bar is having a slightly less nerdy good time.
But in fact, it goes even further. There are several whole fields of mathematics devoted to billiard balls.
For example, mathematicians have shown that you can arrange billiard tables and billiard balls in all sorts of interesting shapes and configurations to get all sorts of interesting results. You could have many billiard tables, joined up by narrow passages, like pipes or tubes, forming patterns. You can have billiard tables designed to keep billiard balls rolling about for a while and then come out through a tube. You can have billiard tables with incoming and outcoming tubes, and a billiard ball comes out this tube if balls comes in both those tubes.
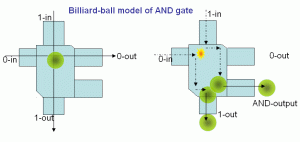 (Source)
(Source)
Here is a picture of a billiard table which functions as an AND gate, which is something you see in electronic circuits and in computers. In fact, you can make computers out of billiard balls.
Of course, it’s a hypothetical computer where we assume that all the billiard balls move without friction and never slow down and don’t spin and so on. But mathematicians are happy to make those assumptions, we are not limited by those kinds of practical considerations. But under those assumptions, you can arrange a billiard table to do the things a computer can. Here’s the Wikipedia article on it.
And here is a book on mathematical billiards.

Here’s its table of contents.

Do you recognise any of the maths there? I’m struggling, and I do this stuff for a living!
It gets into some of the most advanced and cutting-edge areas of mathematics.
And this is just one sub-sub-sub field of contemporary mathematics. Mathematicians take an idea, like a billiard table, think up some problems, solve them, and develop entire theories out of their pure imagination and curiosity.
So maybe some mathematicians have too much time on their hands.
But who knows? Perhaps this mathematics one day will be used to design solar panels – after all that’s all about reflecting light rays cleverly, just like a pool player bounces balls off walls cleverly. Or who knows what else. Or perhaps not. History is full of examples of mathematicians thinking up maths for its own sake, which then later on turns out to be useful in a completely unforeseeable kind of way.
If their maths gets used for something useful, the mathematicians who invented it will be very happy; but, if it doesn’t, they won’t be particularly disappointed.
That’s how mathematics works. It is, by far, the craziest and most unpredictable of the sciences, and I think the most fun and the most profound.
* * *
It’s interesting, for instance, to consider from this point of view a subject that by now most of you – maybe all of you? –have studied: calculus.
Who discovered calculus? These two gentlemen.


(Source: Wikipedia x 2)
Calculus was discovered at roughly the same time by two different people: Isaac Newton (left), and Gottfried Wilhelm Leibniz (right). Newton was English, Leibniz was German, and who came first was a matter of national pride and a lot of controversy.
Online there is a comic called XKCD. It has nerdy maths jokes in it. Here’s one about the discovery of calculus.
 (Source)
(Source)
Get it? Because a derivative is a thing in calculus, but also, when someone takes an idea someone else has, it’s called…
Anyway, so let’s consider the discovery of calculus.
It is an enormous advance in knowledge to be able to use calculus. Using differential calculus, you can figure out, merely from knowing the position of an object, how fast it is moving, at any instant of time. You can then calculate the exact trajectory of an object – so you can work out the motions of objects, of any size, from billiard balls, to the motions of the stars, to… Angry Birds.
But the discovery of calculus was very controversial – not only for the priority dispute between Newton and Leibniz. It was also controversial because it made no sense. Do you remember your dy/dx, and wondering what the dx and the dy mean? The derivative dy/dx tells you how much y changes compared to how much x changes. But what is this dx and this dy? They are supposed to represent really small changes in x and y. But how small? Really small – infinitesimally small – smaller than any positive number – and yet not zero.
Newton and Leibniz both had incredible intuitions about these things. They knew what they were doing, and knew how to use calculus – and yet they couldn’t quite express their theories in a sufficiently rigorous way to satisfy their colleagues. They were mocked for producing these inconsistent things which were infinitesimally small and yet not quite zero and if not quite zero but not any definite number more than zero then what? Their colleagues asked WTF.
Later, the ideas of calculus were put on a logically firm footing – today it’s on firm ground. This was largely done with the idea of limits – and today, at school, when you learn calculus, you learn about it via limits. This definition of the derivative, which you’ve hopefully seen, comes much later – it was not how Newton or Leibniz did it.
But if you’ve ever felt that the dy and the dx are really weird and what the hell is going on here and am I really getting the full story – then I applaud your scepticism and you are in excellent company and you can get the full story with further study – although it’s not an easy story and there’s a reason it’s left to university. There’s a whole world of mathematics that comes from considering these ideas further — and that mathematics is crucial in engineering and physics and much more.
Newton invented calculus, actually, not out of pure curiosity, but because he wanted to understand the motion of the planets. It was physics that motivated him. And he made enormous breakthroughs by applying calculus to the problem.
Calculus is an intellectual superpower. And today, everyone who learns calculus receives the benefit of this superpower. You all have the power to calculate how fast something is going merely from knowing its position as a function of time. Tell us where something is, and we can tell you where it is going. Nobody had that power until 300 years ago, and today it has become completely routine. Although the awesomeness of your superpower may become a little lost on you as you differentiate six hundred slightly different functions from your mathematics textbook.
And of course, our mathematical superpowers have grown enormously since the 17th century.
We now know how to use mathematics to see how matter bends space and time. We use mathematical superpowers to move gigabytes of information in mere seconds around the world – and yet invisibly, so that all you see of it is a cat video.
We use mathematical superpowers to encrypt our messages so that even if we broadcast our encrypted message to the world, put it on display, and even broadcast how we encrypted it, then all the computing power in the world is not enough to decode our message.
Mathematics can do all this, and we are still figuring things out.
I like to think of mathematics as a brain extension. Mathematics is a brain extension that allows you to solve some problems you never thought you could. And it’s being developed further all the time.
* * *
And that leads to a philosophical question, which you may have discussed in your theory of knowledge course. What is mathematical knowledge? Whatever it is, it’s a different type of knowledge to almost anything else.
When we say that 1+1=2, we’d say that’s a true statement. It’s not very controversial. That’s mathematical knowledge.
But if we said that 1+1=3, we’d be pretty well justified in saying it’s false. That’s not very controversial either. That’s also mathematical knowledge, a known falsehood.
And this truth and falsehood is in a kind of absolute sense.
And there are of course many other mathematical truths. That’s what mathematics consists of. All the mathematical theorems and facts you’ve learned at school so far are mathematical truths.
So let’s look at one piece of mathematical knowledge, which is really nice: Pythagoras’ theorem.
Remember what Pythagoras’ theorem says?
Pythagoras’ Theorem:
In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

(Source)
Yes, but can you prove it?
Actually there are many many ways to prove Pythagoras’ theorem. It’s probably the most proved theorem ever. There are books consisting entirely of hundreds of different proofs of Pythagoras’ theorem. I’ll show you one of my favourites, which is similar to a one given by Bhaskara, an Indian mathematician who lived in the 12th century AD.
It’s a proof by animated GIF.
 (Source)
(Source)
This animation I think shows really nicely what’s going on. Now to give a proof you should write an actual argument, and explain why when you swing the triangles around they make the arrangement shown. But that’s not too hard. I think you can get a lot out of this picture.
But I think, if you understand this picture – and you might have to stare at it for a while to fully understand it – then you will understand that the certainty with which we believe Pythagoras’ theorem to be true is a similar level of certainty as we believe that 1+1=2.
So this is another example of a mathematical proof – a type of knowledge which is arguably the most certain thing in the world.
* * *
So 1+1=2, Pythagoras’ theorem, and other mathematical theorems, all have this kind of absolute truth about them. The level of knowledge contained in them is very different from other statements.
Are there any statements outside of mathematics which have a similar status of absolute truth?
Well, there are facts about the world, which are pretty certainly true. There is a chair here, today is sunny, Donald Trump is the President-Elect of the United States. The last one may be hard to believe, but that doesn’t make it any less true. They’re all empirical facts.
Still, I wouldn’t say they quite have the same level of certainty as 1+1=2. We might debate what sunny means, about the technicalities of US elections. And we might be wrong about them. We say it’s sunny, but this is Melbourne, so it might spontaneously cloud over and rain in a few minutes. Perhaps it will be discovered tomorrow that there was a giant conspiracy to rig the US election. There are also more radical ways we could be wrong. Perhaps there is not in fact a chair here and my eyes are deceiving me. Perhaps I am hallucinating. Perhaps we are all hallucinating. Perhaps this is all a dream. All these things are very unlikely, but in a certain sense, not entirely inconceivable.
On the other hand, is it ever possible that 1+1=2 could be falsified?
Scientific facts and theories also have a very high status as knowledge. But even scientific facts and theories are falsifiable. In fact, this is the whole point of scientific theories: they should be able to be confirmed or disproved. Even the most well-established theories can turn out to be wrong. Newton’s theory of gravity works to a very high level of precision, but turns out it’s wrong – it was superseded by Einstein’s theory of relativity, which makes different predictions, and when they differ Newton is wrong and Einstein is right. Relativity might be superseded in due course. Every scientific fact is just as weak as the next experiment, and if the next experiment doesn’t agree with the theory, it could all come tumbling down.
But could you imagine that one day an observation will contradict 1+1=2, and that in fact it might turn out to be a tiny bit more than 2? Not really. It’s an interesting question why, and nailing down the certainty of mathematics is a topic which has occupied some of the greatest minds in mathematics and philosophy – people like Descartes, Bertrand Russell, and Kurt Gödel.
So there’s a certain sense in which mathematics is the most certain type of knowledge. One might even define mathematics as the thing that produces certain knowledge.
But the type of knowledge that you get from mathematics is limited. It can tell you many things about numbers, or polynomials, or geometry, but perhaps not so much about, say, morality, or justice, or a good life, or love. Perhaps it might contribute something, but not much.
Actually my favourite nerd-comic, XKCD again, has a good one about mathematics and love.
 (Source)
(Source)
A mathematician has some tools that can be used to analyse many things. But alas, it doesn’t take you very far here. Although there is a recent book by Hannah Fry called “The Mathematics of Love”, which is lots of fun.

(Source)
* * *
A related question is about what type of thing mathematics is. When the ancient Greeks wrote down the first proofs of Pythagoras’ theorem, were they inventing it, or discovering it?
With science, we speak of scientific discovery, not invention. We discover the law of gravity, or the laws of optics, or whatever. We don’t invent it. The law was already there; humans just figured it out.
When we speak of invention, we mean something that is made by humans, created by human ingenuity. We invent the steam engine, the transistor, the iPhone, and so on. The invention wasn’t there before; humans brought it into being.
When mathematicians prove new theorems, is it like discovering the law of gravity, or inventing the iPhone?
A lot of mathematicians, in describing how they solve problems and prove theorems, will talk about discovery rather than invention. Pythagoras’ theorem was true before they proved it; they just found a proof.
In that case, mathematics already exists. As we gain more knowledge about it, we discover it, just like the laws of nature.
If you’ve ever solved a hard maths problem, you might have had a feeling that everything finally made sense, that it all became clear, you finally “saw” it. And that kind of feels like you were discovering something, or finally seeing something clearly that was already there. Often in maths we find that there is a nice answer that “really” explains what’s going on – perhaps like that proof of Pythagoras we saw before. And then we talk about “finding” or “discovering” the solution, rather than inventing it.
This sort of approach is often associated with the ancient Greek philosopher Plato – and called Platonism. Platonism is then basically the view that abstract objects exist. When we say that 1+1=2, what are we saying? It seems that we are saying that there are numbers, 1 and 2, and when we add the 1 to itself we get 2. But then what are these things called numbers? The Platonist says that, you know what they are, they exist and they are ideal objects. They are not objects you can touch, but they exist just as well. They are not just in our minds. If there were no humans in the universe, or anyone to think it, it would still be true that 1+1=2. So, a Platonist would say, the numbers 1 and 2 exist.
And similarly, the Platonist would say, not just 1 and 2, but every single number exists. They are all mathematical things. Similarly, abstract triangles, sets, functions and so on all exist. Every abstract mathematical object exists.
So, that’s one view, Platonism.
A contrary, anti-Platonist view, which sometimes goes by the name of nominalism, is that no, there is no heaven somewhere containing all these objects. Where would it begin and where would it stop? Mathematics can think up all manner of abstract objects, and if all of them exist, eternally and regardless of whether we think of them, then this is just an enormous parallel universe littered with mostly useless abstract objects, all adding very little except confusion.
Well, fair enough, but then the nominalist has to answer the question: If 1 and 2 are not things that exist, then what are they?
So, suppose you’re asked to explain why 1+1=2. What do you say?
If you’re a normal person, you might say something like, when I have one thing and I put it together with another thing I get two things. If you do this, it’s pretty much a nominalist point of view. You’re not arguing that the numbers are pre-existing things. On this view, numbers are just a sort of generalisation – an abstraction from everyday observations. We made the generalisation a long time ago, probably in our infancy, from collections of objects, to numbers. On this view, numbers are just these really cool abstract ideas, ideas in our heads, useful to count things.
If you’re not a normal person but a mathematician, and you’re asked to explain why 1+1=2, then you might start by answering like the normal person, but if you’re pressed on the point, you might take a different tack. You might fall back on definitions. You might go back to a definition of 1, and a definition of 2, and a definition of addition and equals, and then explain why, when you put all these definitions together and make a few deductions, you get an explanation as to why the statement 1+1=2 is true. So the whole thing becomes a big exercise in definitions, and you have to make sure of what your definitions are and why they all fit together – and in the end, the whole thing is just a tautology. 1+1 = 2 because we defined 1 and 2 and + and = in such a way that 1+1=2 is true. This approach sometimes goes by the name of formalism, because it relies on formal definitions.
Now this might seem bizarre. Is it really possible to define the number 1? Is it possible to define addition? Aren’t these just the basic concepts in mathematics? And also, don’t you have to define things in terms of simpler things? How far back can you go? How simple is simple enough? Where does it all end?
Well many mathematicians have thought about this, and there are mathematicians who have devoted a huge amount of time to building mathematics up from the simplest of foundations. In the early twentieth century, two mathematicians thought about it a lot.


(Sources: Bertrand Russell Society, Wikipedia)
These two guys are Bertrand Russell and Alfred North Whitehead. They were both leading mathematicians of the early 20th century. Russell was also a very famous philosopher and author and socialist and educator and peace activist and many other things – probably one of the most impressive human beings of the 20th century. He arguably literally saved the world during the Cuban Missile crisis in 1962, but that’s a whole other story.
These two mathematicians thought very long and hard about how to define mathematics from the very beginnings, from simple, obvious – even more obvious than 1+1=2 – propositions called axioms. And then to deduce the whole of mathematics from that.
They wrote an enormous series of books, 3 volumes, 2000 pages. It was called Principia Mathematica. There it is.
 (Source)
(Source)
And in these 2000 pages they make every single definition and axiom and deduction absolutely clear and explicit. And eventually, they manage, after 700 pages or so, to prove that 1+1=2. Here’s the key part of the proof.

Looks like alien hieroglyphics doesn’t it? But yes, after nearly a thousand pages, these mathematicians proved that 1+1=2.
Well you can now relax.
You might wonder if these guys had anything better to do. Well, actually Bertrand Russell as I mentioned had lot of things of other things to do as well, but he thought this was at least as important!
So, anyway, if you asked me to explain why 1+1=2, and pressed the point, I would eventually point you back to this work of Russell and Whitehead – Principia Mathematica.
And this is really the modern approach in mathematics. A mathematician these days will often write their proofs by making formal definitions of whatever she’s talking about, and then deducing things about them. These objects might or might not relate to the real world; sometimes they do, and sometimes they do not. When they do that’s great; when they don’t, it’s not a great disappointment.
And that is roughly my view. I’m not a Platonist, I’m a nominalist, and a pretty formalist one when it comes down to it. But there are plenty of mathematicians who are Platonists. When you solve a maths problem, I would say, it might feel like you’re uncovering something from the Platonic heaven of universal ideas, but if you feel that way, I’d say that’s just because mathematics is a wonderful subject.
* * *
OK, well that’s all pretty heavy stuff.
Let’s talk about some actual living mathematicians. Most people don’t know any mathematicians alive today, so let me introduce you to a few leading ones.
 (Source)
(Source)
This is Grigori Perelman. He won the Fields Medal in 2006. The Fields Medal is the maths equivalent of a Nobel Prize. He works in a field of mathematics not so far from my own. He is an interesting guy – friend of one of my PhD supervisors.
Anyway, Perelman solved one of the hardest outstanding problems about 3-dimensional space, called the Poincare conjecture, about 10 years ago. I’m not going to try to explain it to you here, but it’s a fundamental problem, but really hard, really fundamental, and there was actually a million dollar prize for anyone who could solve it. He solved it. He then got famous, was in the media a lot, and he didn’t like being paraded in the media. He decided that the community of mathematicians was corrupt, and turned down the million dollar prize. He currently, so far as I know, lives as a hermit with his mother in St Petersburg.
Mathematicians are often interesting characters.
Here’s another interesting character.
 (Source)
(Source)
This is Edward Witten. He is a physicist, perhaps most famous for his work on string theory. But he also won the Fields medal, in 1990, because in doing physics he also did a lot of mathematics. And it’s mathematics which people are still trying to figure out, myself included. Perhaps you can think of what he’s doing, as like Newton or Leibniz with calculus in the 17th century. I read his papers and I have no idea what he’s talking about. Some mathematicians think Witten is sloppy, and talking a lot of nonsense. But then when it comes down to mathematical statements, and calculations, you tend to find out that he’s right. It’s incredible intuition which somehow almost transcends mathematics. By all accounts he’s a very nice guy, and an absolute machine. Is what he does mathematics? It’s not the traditional way of doing mathematics, and not all mathematicians think it is, but I think it is. Just like calculus was hard to digest back in those days, some of Witten’s work isn’t quite yet digestible as maths.
Ed Witten actually studied history at university. He got a degree in history. Then he dropped out of that and decided he wanted to do… economics. Then he dropped out of that too and worked in…. politics. He worked on a losing campaign. They he turned to… maths, but dropped out of that too. Finally he turned to physics. And today he’s probably the most influential physicist alive.
And here’s another famous mathematician.
 (Source)
(Source)
This is Maryam Mirzkhani. She’s an Iranian mathematician, and another Fields Medallist. She works in a field, again, not so far from what I do. She is a great role model for women wanting to study science and mathematics.
* * *
Let me tell you about some of the things I do in my daily life as a mathematician.
As I said, I’m a lecturer at Monash Uni. So one thing I do is lecturing. I teach classes. I give lectures on mathematics. So if you come to Monash uni and study mathematics, you might be in one of my lectures. And if you go on to major in mathematics, you could take my course in differential geometry. If you go on to do honours in mathematics, I might end up teaching you topology. So that’s one thing I do, which is pretty good fun. At least it is for me! And for students, maybe, sometimes!
I also do mathematical research. I work in pure mathematics. As I’ve mentioned to you, as with the billiard balls, pure mathematical research is research that is done purely for its own intrinsic interest. It may have applications, or it may not; but we think it sufficiently interesting and important to develop new fundamental knowledge.
Mathematical research is like mathematical problem-solving, except you get to think up the problem as well as the answer. And if you solve a problem that nobody has ever solved, or even asked, before, then they have progressed human knowledge. And a lot of mathematics develops in this way.
So those are some of the things I do as a mathematician. But I’m not the only type of mathematician.
Many mathematicians also work on research which is much more applied. They tend to make a lot more progress than I do. They don’t beat their head against a wall with impossible problems like I do. Their research has direct practical applications and can affect people’s everyday lives.
Applied mathematics is often motivated by a concrete practical problem, and devising new practical solutions.
And there are many different types of applications. There are mathematicians who apply their mathematics to all sorts of things: chemistry, biology, data analysis, finance, transport, consulting, programming, economics, energy, engineering, government, health, insurance, meteorology, military, intelligence, logistics, biotechnology, teaching – of course, as your maths teachers do here – and much more. Maths is everywhere.
There are also many people who use maths as a large part of their job, but who may not actually call themselves “mathematicians”. They might be setting up mathematical models to simulate a practical situation. They might be making predictions based on such models. They might be running algorithms. They might be coding. They might be analysing data, or calculating statistics, or optimising a manufacturing process or transport network or energy flow. They’re all using maths to solve real world problems. Mathematical skills, and the creative logical thinking skills of mathematicians, are sought after by employers everywhere
So, maths is powerful. It can be used to do many things, and improve the power that we have to do things. It’s a superpower. Like all superpowers, it can be used to achieve all sorts of social ends, good or bad. It can be used to match up organ transplant recipients and save lives. It can be used in war to produce more efficient death. It can be used to optimise a transport network for maximum efficiency. It can also be used to optimise a coal mine for maximum extraction. It can be used to locate tumours and treat cancers. It can also be used to build bigger and more lethal weapons. It can be used to create a more equitable economic system. It can also be used to crash Wall Street.
It’s a big powerful thing, and like all science it can be used for all sorts of ends. I hope you enjoy it, and that you’ll put it to good use.





















